- FMA
- The Fabricator
- FABTECH
- Canadian Metalworking
Categories
- Additive Manufacturing
- Aluminum Welding
- Arc Welding
- Assembly and Joining
- Automation and Robotics
- Bending and Forming
- Consumables
- Cutting and Weld Prep
- Electric Vehicles
- En Español
- Finishing
- Hydroforming
- Laser Cutting
- Laser Welding
- Machining
- Manufacturing Software
- Materials Handling
- Metals/Materials
- Oxyfuel Cutting
- Plasma Cutting
- Power Tools
- Punching and Other Holemaking
- Roll Forming
- Safety
- Sawing
- Shearing
- Shop Management
- Testing and Measuring
- Tube and Pipe Fabrication
- Tube and Pipe Production
- Waterjet Cutting
Industry Directory
Webcasts
Podcasts
FAB 40
Advertise
Subscribe
Account Login
Search
Bumping up large-radius bends
- By Steve Benson
- May 30, 2002
- Article
- Bending and Forming
 |
| Figure 1 |
It often is impractical to buy or build a custom tool just for large-radius bends. Perhaps it is a one-of-a-kind part, or the radius that needs to be produced is too large to be done practically in a single punch and die set.
While rolling the bend in a slip roller always is an option (if you have one), rolling is not the most accurate way to place a large radius in a precision part.
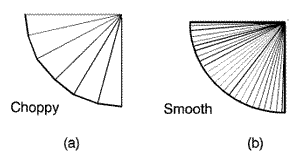
The best option may be to use a step-bending process. Step bending is a procedure in which multiple hits (bends) are made along the entire length of the inside radius to produce the bend. The number of hits used in this process will determine the tooling selection, smoothness of the final surface, and the depth of penetration into the V die. Obviously, the greater the number of hits, thesmoother the outside surface of the radius will be (see Figure 1).
Arc Length
If you use the step-bending process to produce the part, the first thing to determine is the length of the arc. The arc is the measured distance along the inside radius, the distance from the beginning to end of the radius, which may or may not be 90 degrees of bend angle. The following formula can be used to develop that value, where A equals the number of bends and Ir equals the insideradius.
Arc length = 2(pi) x Ir x [(180 - A)/360]
Example: 3.000-inch radius at 45 degrees
6.283185307 x 3.000 x 135/360
18.84955592 x 137 / 360
Arc length = 7.068
Steps and Pitch
The next step is to determine the radius pitch, which is the distance between the bends (or the number of steps required). First, decide which is the priority--the number of steps or the distance between hits. Is a smooth outer surface the priority, or is the speed of production the priority?
If the radius pitch for a bend's number of steps is the most important factor, the following formula may be used:
Radius pitch = Arc length/the required number of hits
If the pitch is more important than the number of hits (bends), use the following equation:
Number of steps = Arc length/pitch
The Leg
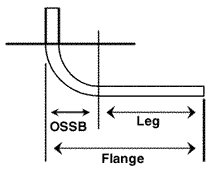 |
| Figure 2: The Outside Setback or X factor is calculated by using the following empirical formula: OSSB = (Tangent (A/2)) x (Material Thickness + Inside Radius) |
The final piece of the puzzle is the leg.
A leg is the flat distance from the edge of the part to the beginning of the radius. This leg also may include other bends not yet formed or, in some cases, bends already in place.
To find the value of the flat from the outside surface of the larger radius to the edge or next feature, an outside setback (OSSB), or X factor, needs to be removed first, as in Figure 2.
The starting point for the step bend is found by adding the leg dimension to the arc length. For press brake controllers without a radius bend or step-bend function each additional step (hit) from the starting point is one radius pitch value less than the previous hit.
Individual Step-bend Angle and Die Width
Determining the required bend angle for each individual hit is a simple matter of dividing the number of degrees in the final bend angle by the number of step to be used:
Per bend angle = Bend angle A/Number of steps
 |
| Figure 3 |
Determining the correct V die width follows a different process than normally would be used. Under normal circumstances a V die is calculated at about eight times the material thickness, in which a one-to-one relationship between the material thickness and inside radius is maintained. When selecting a V die for bump radius bends, choose the value that is equal to twice that of the radiuspitch.
Vee die width = Radius pitch x 2
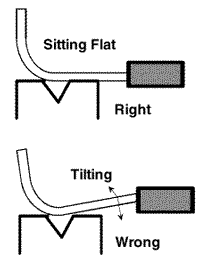
The reason behind this different die width method is best described by Figure 3.
With a V die width that is no greater than twice the radius pitch, the material that already has been bent will not rock into and out of the die space. To ensure the utmost quality and consistency in the final radius, it is imperative that the radius pitch (location) be maintained. If pitch consistency is not maintained, wide variations in both the final radius and bend angle will result.
Consistency of bend angle over the length of the bend also is a concern. Should a "canoe" (a bend angle that opens in the center) occur, it must be corrected before the first pieces are run. If it is not, both the radius and the bend angle will be affected, to the detriment of the finished piece.
While a nice bumped radius may be time-consuming to make on a part-to-part basis, the final result will more than justify the time, especially when compared to the cost of building or buying a custom tool.
About the Author

Steve Benson
2952 Doaks Ferry Road N.W.
Salem, OR 97301-4468
503-399-7514
Related Companies
subscribe now

The Fabricator is North America's leading magazine for the metal forming and fabricating industry. The magazine delivers the news, technical articles, and case histories that enable fabricators to do their jobs more efficiently. The Fabricator has served the industry since 1970.
start your free subscription- Stay connected from anywhere

Easily access valuable industry resources now with full access to the digital edition of The Fabricator.

Easily access valuable industry resources now with full access to the digital edition of The Welder.

Easily access valuable industry resources now with full access to the digital edition of The Tube and Pipe Journal.
- Podcasting
- Podcast:
- The Fabricator Podcast
- Published:
- 04/16/2024
- Running Time:
- 63:29
In this episode of The Fabricator Podcast, Caleb Chamberlain, co-founder and CEO of OSH Cut, discusses his company’s...
- Industry Events
16th Annual Safety Conference
- April 30 - May 1, 2024
- Elgin,
Pipe and Tube Conference
- May 21 - 22, 2024
- Omaha, NE
World-Class Roll Forming Workshop
- June 5 - 6, 2024
- Louisville, KY
Advanced Laser Application Workshop
- June 25 - 27, 2024
- Novi, MI































