- FMA
- The Fabricator
- FABTECH
- Canadian Metalworking
Categories
- Additive Manufacturing
- Aluminum Welding
- Arc Welding
- Assembly and Joining
- Automation and Robotics
- Bending and Forming
- Consumables
- Cutting and Weld Prep
- Electric Vehicles
- En Español
- Finishing
- Hydroforming
- Laser Cutting
- Laser Welding
- Machining
- Manufacturing Software
- Materials Handling
- Metals/Materials
- Oxyfuel Cutting
- Plasma Cutting
- Power Tools
- Punching and Other Holemaking
- Roll Forming
- Safety
- Sawing
- Shearing
- Shop Management
- Testing and Measuring
- Tube and Pipe Fabrication
- Tube and Pipe Production
- Waterjet Cutting
Industry Directory
Webcasts
Podcasts
FAB 40
Advertise
Subscribe
Account Login
Search
Fundamentos para la aplicación de las funciones de doblez
Cálculo de la holgura de doblez, reajuste exterior y deducciones de doblez
- February 22, 2013
- Article
- Bending and Forming
Cuando se dobla una parte de hoja metálica, ésta se hace físicamente más grande. Las dimensiones finales de la pieza formada serán mayores que la suma total de las dimensiones exteriores de la parte mostradas en el plano—a menos que se deje una holgura para el doblez. Muchos dirán que el material “crece” o “se encoje” al ser doblado en una prensa. Técnicamente, el metal no experimenta nada de esto, más bien se alarga. Lo hace porque el eje neutro se recorre hacia la cara interior del material.
El eje neutro es un área dentro del doblez en la cual el material no sufre cambios físicos durante el formado. Al exterior del eje neutro el material se expande; al interior del eje neutro el material se comprime. A lo largo del eje neutro, no hay cambios—ni expansión ni compresión. Conforme el eje neutro se recorre hacia la cara interior del material, se expande más material al exterior que el que se comprime al interior del eje neutro. Ésta es la causa raíz de la recuperación elástica.
Holgura de Doblez (BA)
BA = [(0.017453 × Radio interior) + (0.0078 × Espesor del material)] × Ángulo de doblez, que es siempre complementario
La longitud del eje neutro se calcula como una holgura de doblez, tomada al 50 por ciento del espesor del material. En el Machinery’s Handbook, el factor K para el acero suave laminado en frío con resistencia a la tensión de 60,000 PSI, es de 0.446 pulgadas. Este factor K se aplica como un valor promedio para la mayoría de los cálculos de holgura de doblez. Hay otros valores para acero inoxidable y aluminio, pero en la mayoría de los casos, el valor de 0.446 pulgadas funciona bien en casi todos los tipos de material.
Si se multiplica el espesor del material por el factor K (0.446), se obtiene la ubicación del eje neutro desplazado: por ejemplo, 0.062 × 0.446 = 0.027 pulgadas. Esto quiere decir que el eje neutro se mueve del centro del material a un punto ubicado a 0.027 pulgadas de la cara del radio de doblez interior. Nuevamente, el eje neutro no sufre cambios físicos, ni estructural ni dimensionalmente, simplemente se mueve hacia la cara interior, causando un alargamiento.
Observe los dos factores mostrados en la fórmula para la holgura de doblez: 0.017453 y 0.0078. El primer factor se usa en círculos o partes de un círculo, y el segundo valor aplica el promedio del factor K al primer factor. 0.017453 es el cociente de π/180. 0.0078 viene de (π/180) × 0.446. Observe que para la holgura de doblez, el ángulo de doblez se mide siempre como complementario (vea la Figura 1).
Reajuste Exterior (OSSB)
OSSB = [Tangente (Grado del ángulo
de doblez / 2)] × (Radio de doblez interior + Espesor del material)
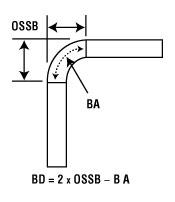
Figura 2: El reajuste exterior (OSSB) es un valor dimensional que empieza en la tangente del radio y la parte plana de la pierna, y termina en el ápice del doblez.
El reajuste exterior es un valor dimensional que empieza en la tangente del radio y la parte plana de la pierna, midiendo hacia el vértice del doblez (vea la Figura 2). A 90 grados, no importa si usa el ángulo incluido o el complementario; usted acabará con 45 grados y obtendrá el mismo resultado de OSSB.
Para ángulos sub-doblados (vea la Figura 3), es una práctica común usar el ángulo complementario. Para ángulos sobre-doblados (doblez agudo), puede usarse el ángulo incluido o el complemen-tario. La elección depende de usted, pero sí afectará la forma en que usted aplique los datos al patrón plano.
Deducción de Doblez (BD)
BD = Reajuste exterior × 2) – Holgura de doblez
Una deducción de doblez (BD) es el valor restado de la pieza plana para cada doblez en la parte, y puede haber más de una. Las deducciones de doblez difieren dependiendo de la parte en sí, diferentes ángulos de doblez y/o radios interiores. Observe que al sobre-doblar y calcular el OSSB usando el ángulo de doblez incluido, puede calcular un valor negativo para la deducción de doblez. Usted necesitará considerar el valor negativo al calcular la pieza plana, que se trata en la siguiente sección.
Desarrollo del arreglo de la pieza plana
Hay dos maneras básicas de disponer una pieza plana, y cuál se usará dependerá de la información con que usted cuente. Para el primer método, necesita saber las dimensiones de la pierna. Una pierna es un área plana de una parte, ya sea entre radios de doblez o entre una orilla y un radio de doblez. Para el segundo método, necesita saber la dimensión de la orilla (formada o cortada) al ápice del doblez, o la intersección creada por ambos planos que van paralelos a las caras exteriores del material formado.
1. Pieza plana = Dimensión de la primera
pierna + Dimensión de la segundapierna + Holgura de doblez
2. Pieza plana = Dimensión hasta el ápice
+ Dimensión hasta el ápice –
Deducción de doblez

Figura 3 La terminología puede variar dependiendo de cómo se lea el transportador. Este artículo define “sub-dobleces” como aquéllos con ángulos incluidos de más de 90 grados. “Sobre-dobleces” (también llamados dobleces agudos) son aquellos con ángulos incluidos menores a 90 grados.
Hay otra forma de ver la segunda opción. Como ya se mencionó anterior-mente, si usted usa el ángulo incluido para el OSSB, la deducción de doblez puede ser un valor negativo. Como usted probablemente sabe, restar un valor negativo requiere que sumar: por ejemplo,
10 – (– 5 ) = 15. Si usted está haciendo el cálculo con su calculadora, ésta hará los cálculos correctos automáticamente. Si usted está aplicando la fórmula paso a paso, necesitará tener en cuenta si el resultado es positivo o negativo.
Los siguientes ejemplos lo guiarán a través de los métodos de desarrollo de piezas planas. Éstos aplican funciones de doblez a un parte simple de un solo doblez, doblada a un ángulo complementario mayor a 90 grados, para mostrar cómo se aplican los ángulos complementarios o incluidos al OSSB y en última instancia a un arreglo.
La parte en la Figura 4 está doblada a un ángulo complementario de 160 grados. Tiene un espesor de material de 0.250 pulgadas y un radio de doblez interior de 0.250 pulgadas. Cada pierna es de 1.000 pulgadas, y la dimensión al ápice (entre la orilla de la parte y el ápice del doblez) es 3.836 pulgadas. Observe que en las siguientes fórmulas, Ir representa el radio de doblez interior y Mt representa el espesor del material. Para todos los métodos, calculamos la holgura de doblez de la misma manera:
Holgura de Doblez (BA)
BA = [(0.017453 × Ir) + (0.0078 × Mt)] × Grado del ángulo complementario de doblez
BA = [(0.017453 × 0.25) + (0.0078 × 0.25)] × 160
BA = [0.00436325 + 0.00195] × 160
BA = 0.00631325 × 160
BA = 1.010
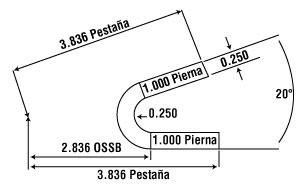
Figura 4: Esta parte de 0.250 pulgadas de espesor es doblada a un ángulo complementario de 160 grados con un radio de doblez interior de 0.250 pulgadas. El dibujo especifica que la dimensión de la orilla al ápice es 3.836 pulgadas.
De aquí, hacemos diferentes cálculos, dependiendo del desarrollo de pieza plana usado. Usando el primer método, desa-rrollamos la pieza plana sumando las dos piernas del doblez y la holgura de doblez.
Cálculo de la pieza plana
Longitud de la pieza plana calculada = Pierna + Pierna + BA
Longitud de la pieza plana calculada = 1.000 + 1.000 + 1.010
Longitud de la pieza plana calculada = 3.010
El segundo ejemplo de desarrollo de pieza plana suma las dos dimensiones (de la orilla al ápice), y resta una deducción de doblez. En este caso, los cálculos usan un ángulo complementario para el OSSB, y las dimensiones son tomadas desde la orilla al ápice—Nuevamente, como se especifica en la Figura 4.
Reajuste Exterior (OSSB)
OSSB = [Tangente (ángulo complementario de doblez /2)] × (Mt + Ir)
OSSB = [Tangente (160/2)] × (0.25 + 0 .25)
OSSB = [Tangente 80] × 0.5
OSSB = 5.671 × 0.5
OSSB = 2.836
Deducción de Doblez
BD = (OSSB × 2) – BA
BD = (2.836 × 2) – 1.010
BD = 5.672 – 1.010
BD = 4.662
Cálculo de la pieza plana
Pieza plana calculada = Dimensión al ápice + Dimensión al ápice – Deducción de doblez
Pieza plana calculada = 3.836 + 3.836 – 4.662
Longitud de la pieza plana calculada = 3.010
En este ejemplo final, el cálculo de la pieza plana suma las dimensiones y luego resta la deducción de doblez negativa (nuevamente, al restar un número negativo usted debe sumar). En este caso, estamos usando el ángulo incluido para el OSSB, y las dimensiones siguen tomándose desde la orilla hasta el ápice.
Reajuste Exterior (OSSB)
OSSB = [Tangente (Grado del ángulo incluido de doblez /2)] × (Mt + Ir),/i>
OSSB = [Tangente (20/2)] × (0.25 + 0.25)
OSSB = [Tangente 10] × 0.5
OSSB = 0.176 × 0.5
OSSB = 0.088
Deducción de Doblez (BD)
BD = (OSSB × 2) – BA
BD = (0.088 × 2) – 1.010
BD = 0.176 – 1.010
BD = -0.834
Cálculo de la Pieza Plana
Pieza plana calculada = Dimensión al ápice + Dimensión al ápice – Deducción de doblez
Pieza plana calculada = 1.088 + 1.088 – (-0.834)
Longitud de la pieza plana calculada = 3.010
Usted puede observar que sin importar el método, se obtiene el mismo resultado. Asegúrese de calcular estos valores con base en el radio real que está obteniendo en la parte física. Hay diversas circunstancias atenuantes que usted puede necesitar considerar. Algunas son el método de formado (formado con aire, embutido o acuñado), el tipo de doblez (dobleces en pico, en radio o en radio profundo), el herramental que esté usando, y las roturas múltiples de la pieza de trabajo durante un doblado de radio grande. Además, mientras más sobrepase los 90 grados, menor será físicamente el radio interior. Usted puede calcular la mayoría, y es algo que seguro trataremos en futuros artículos.
Obteniendo la pieza correcta la primera vez
Hay muchos caminos para hacer un doblez, usando ángulos incluidos o complementarios. Podemos calcular fácilmente estos valores; lo que cuenta es la aplicación de los resultados. Sin embargo, una vez que usted sabe cómo y dónde se aplica la información en una situación dada, el arreglo del patrón plano es fácil.
Entonces, ¿Por qué calcular todos estos valores? Porque a veces usted necesitará trabajar un doblez sobre un plano, y puede no tener toda la información que necesita para completar un patrón plano. Al menos ahora usted puede calcular todas las diferentes partes del doblez, aplicarlas correctamente y hacerlo bien la primera vez.
About the Publication
Compañías Relacionadas
subscribe now

FMA Communications ha introducido al mercado la edición en Español de la revista The Fabricator. Esta versión consiste del mismo tipo de artículos técnicos y sección de lanzamientos de nuevos productos que actualmente presentan el personal de primera categoría de Fabricator en Inglés.
start your free subscription- Podcasting
- Podcast:
- The Fabricator Podcast
- Published:
- 04/16/2024
- Running Time:
- 63:29
In this episode of The Fabricator Podcast, Caleb Chamberlain, co-founder and CEO of OSH Cut, discusses his company’s...
- Trending Articles
La mezcla de gas auxiliar impulsa la tecnología del láser de fibra

Los operadores de prensa dobladora inexpertos hacen indispensable el repensar la seguridad

Nuevas herramientas contribuyen a operaciones de prensa más inteligentes

Máquina de corte por láser diseñada para el mercado mexicano

La sierra de doble carro sigue los contornos del tubo perfectamente

- Industry Events
16th Annual Safety Conference
- April 30 - May 1, 2024
- Elgin,
Pipe and Tube Conference
- May 21 - 22, 2024
- Omaha, NE
World-Class Roll Forming Workshop
- June 5 - 6, 2024
- Louisville, KY
Advanced Laser Application Workshop
- June 25 - 27, 2024
- Novi, MI


























