Contributing Writer
- FMA
- The Fabricator
- FABTECH
- Canadian Metalworking
Categories
- Additive Manufacturing
- Aluminum Welding
- Arc Welding
- Assembly and Joining
- Automation and Robotics
- Bending and Forming
- Consumables
- Cutting and Weld Prep
- Electric Vehicles
- En Español
- Finishing
- Hydroforming
- Laser Cutting
- Laser Welding
- Machining
- Manufacturing Software
- Materials Handling
- Metals/Materials
- Oxyfuel Cutting
- Plasma Cutting
- Power Tools
- Punching and Other Holemaking
- Roll Forming
- Safety
- Sawing
- Shearing
- Shop Management
- Testing and Measuring
- Tube and Pipe Fabrication
- Tube and Pipe Production
- Waterjet Cutting
Industry Directory
Webcasts
Podcasts
FAB 40
Advertise
Subscribe
Account Login
Search
Die Basics 101: Mechanical properties and behavioral characteristics of metals
- By Art Hedrick
- Updated July 18, 2018
- August 8, 2006
- Article
- Bending and Forming
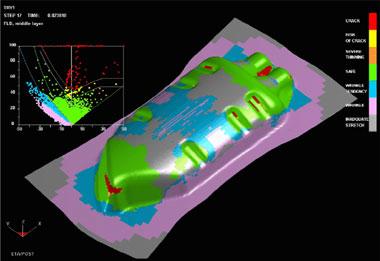 |
| Figure 1 Strain and Thickness Distribution |
Strain
Strain can be defined simply as a measurable deformation of the metal. In other words, metal must be "strained" in order to change its shape. Strains can be positive (pulling the metal apart, or tension) or negative (pushing the metal together, or compression.) Strains also can be permanent (plastic) or recoverable (elastic). The result of elastic straining commonly is referred to as springback, or elastic recovery.
Remember, every metal type wants to return to its original shape when it's deformed. The amount the metal springs back is a function of its mechanical properties. When engineers refer to part areas that are "high strain," they typically are referring to areas that have been subjected to substantial stretch or compression. Figure 1shows a simulation image of a part that has been stretched. Each color represents a different type and amount of strain. Some of the strains are positive and others are negative.
Stress
Stress is simply the result of straining the metal. When subjected to stress, metal incurs internal changes that cause it to spring back or deform nonuniformly. Trapped stresses within a part often result in a loss of flatness or other geometric characteristics. All cut or formed parts incur stress.
Stretch Distribution
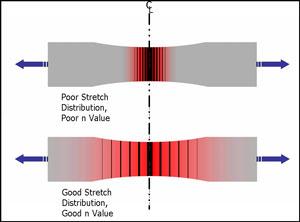 |
| Figure 2 Stretch Distribution / Tensile Test |
Stretch distribution is a very important mechanical property. A metal's stretch distribution characteristics control how much surface area of the stretched metal is permanently deformed. Stretch distribution is determined primarily by checking the metal's thickness when it's deformed in tension during the tensile testing process. The more uniform the thickness distribution, the better the stretch distribution. Stretch distribution also is partially expressed in the metal's n value. Figure 2 shows different stretch distribution results. The red areas of the sample test coupon represent areas that have been stretched.
n Value
To understand n value, otherwise known as the work or strain hardening exponent, you must understand that every time metal is exposed to permanent deformation, work hardening occurs. It's the same thing that happens when you bend a coat hanger back and forth. As you bend the hanger, it gets harder and harder to bend. It also becomes more difficult to bend it in the same place. This increase in strength is the result of work or strain hardening. However, if you continue to bend the hanger in the same spot, it will eventually fail.
Ironic as it may seem, materials need to work-harden to achieve both good stretchability and stretch distribution. How they work-harden is the key. The n value of a material can be defined fundamentally as the metal's stretchability; however, it also is an expression of a material's stretch distribution characteristics.
Perhaps one of the most important mechanical properties to consider if the stamped part requires a great deal of stretch, the n value is expressed numerically in numbers from 0.100 to 0.300 and usually is carried out two or three decimal places. The higher the number, the greater the metal's stretchability and stretch distribution. Higher-strength metals, such as spring steel, have very low n values, while metals such as those used for making oil pans and other deep-formed parts usually exhibit higher n values.
The metal's n value also is a key mechanical value used in creating forming limit diagrams. (This will be discussed in subsequent parts of this series.)
r Value
The metal's r value is defined metallurgically as the plastic strain ratio. To understand this concept, you must clearly know the difference between stretching and drawing. Stretching is a metal forming process in which the metal is forced into tension. This results in an increase in surface area. Items such as most automobile hoods and fenders are made using this process.
Drawing is the displacement of metal into a cavity or over a punch by means of plastic flow or feeding the metal. Items such as large cans, oil pans, and deep-formed parts usually are made using this process.
 |
| Figure 3 Plastic Strain Ratio r Value |
The metal's r value can be defined simply as the metal's ability to flow. It also is expressed numerically using a value from 1 to 2, which usually is carried out two decimal places. The greater the r value, the more drawable the metal (Figure 3).
The metal's r value is not uniform throughout the sheet. Most metals have different r values with respect to the metal's rolling direction. Testing for a metal's r value requires tensile testing in three different directions—with the rolling direction, against the rolling direction, and at 45 degrees to the rolling direction. The test results usually are averaged and expressed as the r bar, or average of the r values.
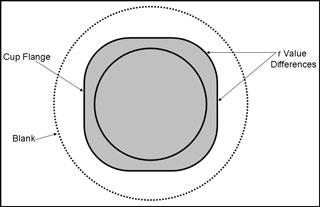 |
| Figure 4 Earring Caused by Differences in the Metal's r Value |
Differences in the plastic strain ratio result in earring of the metal when being drawn. For example, when drawing a round shell from a round blank, the results will be a near square bottom on the flange of the cup. This effect (Figure 4) is caused by different amounts of metal flow with respect to the metal's
Surface Topography
A metal's surface topography, defined simply as the metal surface finish, is created mainly during the metal rolling process. Surface topography is an important metal characteristic. When being drawn, metals often require a surface finish that has the ability to hold lubricant. Surface topography is determined with a measuring tool called a profilometer.
This wraps up the discussion of sheet metal characteristics. The next article in this series will focus on metal cutting.
Editor's Note:
Part I provides an introduction to stamping.
Part II covers various forming operations.
Part III discusses several production methods used to make stamped parts.
Part IV and Part V cover common stamping die components.
Part VI explains specialty die components.
Part VII provides an overview of metals used in stamping, and Part VIII continues this discussion.
Part IX covers the mechanical properties as well as behavioral characteristics of metals.
Part X begins an in-depth look at the metal cutting process.
Part XI defines slug pulling and common causes.
Part XII describes methods for resolving slug-pulling problems.
Part XIII discusses various specialty metal cutting methods used in stamping operations.
Part XIV explains fineblanking and GRIPflow®.
Part XV describes several bending methods—wipe, coin relief, pivot, and V bending.
Part XVI continues the discussion of bending in stamping operations, focusing on rotary and reverse U bending. It also addresses the advantages and disadvantages of rotary bending.
Part XVII discusses the fundamentals of drawing and stretching.
About the Author

Art Hedrick
10855 Simpson Drive West Private
Greenville, MI 48838
616-894-6855
Related Companies
subscribe now

The Fabricator is North America's leading magazine for the metal forming and fabricating industry. The magazine delivers the news, technical articles, and case histories that enable fabricators to do their jobs more efficiently. The Fabricator has served the industry since 1970.
start your free subscription- Stay connected from anywhere

Easily access valuable industry resources now with full access to the digital edition of The Fabricator.

Easily access valuable industry resources now with full access to the digital edition of The Welder.

Easily access valuable industry resources now with full access to the digital edition of The Tube and Pipe Journal.
- Podcasting
- Podcast:
- The Fabricator Podcast
- Published:
- 04/16/2024
- Running Time:
- 63:29
In this episode of The Fabricator Podcast, Caleb Chamberlain, co-founder and CEO of OSH Cut, discusses his company’s...
- Industry Events
16th Annual Safety Conference
- April 30 - May 1, 2024
- Elgin,
Pipe and Tube Conference
- May 21 - 22, 2024
- Omaha, NE
World-Class Roll Forming Workshop
- June 5 - 6, 2024
- Louisville, KY
Advanced Laser Application Workshop
- June 25 - 27, 2024
- Novi, MI































