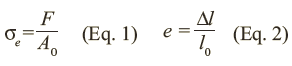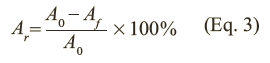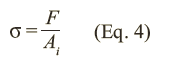Determining the flow stress curve with yield and ultimate tensile strengths, Part I

Important data from the tensile test

May 11, 2011

Yield strength and ultimate tensile strength can be used to determine the flow stress curve. First, the tensile test reveals tensile force and elongation, which are used to obtain the stress-strain curve, which reveals yield stress and ultimate tensile strength.

Editor's Note: Part II of this article will appear in the July/August 2011 issue.

Material suppliers often provide the yield stress and ultimate tensile strength for sheet materials. They don't, however, always provide the true stress-true strain (flow stress) curve. This curve is one of the most important variables for calculating input data for the finite element (FE) and analytical methods used to predict metal flow and defects.

The flow stress curve, which reflects the sheet material's elastic and plastic properties, typically is obtained from a tensile test or bulge test.¹ In a tensile test, a standard-size specimen is cut out from the sheet metal and pulled slowly until it breaks. An extensometer is attached to the specimen to measure the elongation over an original gauge length, l0. Throughout the test, the load applied and the elongation of gauge length are recorded in real time (see Figure 1).

The engineering stress, σe, and the engineering strain, e, are calculated as:

where:

F = tensile force applied to the specimen

A₀ = original cross-sectional area of the specimen

l₀ = original gauge length

Δl = elongation of l₀ during the test

The F versus Δl data is used to obtain the engineering stress-strain curve (see Figure 2), which helps determine several basic mechanical material properties:

• Yield stress (Y) indicates the start of plastic deformation. Y is determined approximately by drawing a parallel line to the linear elastic region of the flow stress curve from 0.2 percent engineering strain. The intersection of this parallel line with the flow stress curve gives the value of Y.
  
  
• Ultimate tensile strength (UTS) is the maximum engineering stress in a tensile test and signifies the end of uniform elongation and the start of localized necking.
  
  
• Elastic modulus (E) (also known as Young's modulus) is the slope of the elastic part of an engineering stress-strain curve.
  
  
• e₀ is the elongation at Y.
  
  
• Uniform elongation, e_u, is the elongation at the maximum load.
  
  
• Total elongation, e_t (also known as elongation at break), is the elongation of the original gauge length of a tensile specimen at fracture, including both uniform (e_u) and postuniform elongations.
  
  
• Area reduction, A_r, is the percentage of reduction in the area, calculated by cross-sectional area at fracture, Af, and initial cross-sectional area, A₀:

The total elongation, e_t, at fracture and the total area of reduction at fracture, A_r, are considered to be indications of material ductility. However, the uniform elongation, e_u, better represents the material's ductility or formability in uniaxial deformation, because after necking (when uniform elongation is exhausted), the material can be considered to have failed.

The stress and strain definitions in Equations 1 and 2 are based on the original cross-sectional area of the tensile specimen, so they are known as engineering stress and strain. True normal stress, σ, is based on the instantaneous cross-sectional area, A_i:

True stress values are more accurate measures of stress than engineering values for large deformations.² True stress can be calculated as:

Similarly, true strain calculation considers the instantaneous gauge length of the specimen, l_i = Δl + l₀, instead of the initial length, l₀:

A flow stress curve does not reach a maximum, as an engineering stress-strain curve does (see Figure 3), because by definition it can be drawn up to the strain value corresponding to the start of necking. For instance, Equations 5 and 6 are valid in the range of uniform elongation, e_u.

Figure 4 shows the flow stress curves for a draw-quality steel (AKDQ), an aluminum alloy (Al 5754), and a high-strength steel (DP600). Force and elongation are the measured values (Figure 1), while the engineering stress-strain curves (Figure 2) and flow stress curves (Figure 3) are calculated using the previous equations.

Nimet Kardes Sever and Xi Yang are graduate research associates, Dr. Changhyok Choi is postdoctoral researcher, and Taylan Altan is professor and director of the Center for Precision Forming (CPF), The Ohio State University, 339 Baker Systems, 1971 Neil Ave., Columbus, OH 43210-1271, 614-292-9267, www.cpforming.org.