- FMA
- The Fabricator
- FABTECH
- Canadian Metalworking
Categories
- Additive Manufacturing
- Aluminum Welding
- Arc Welding
- Assembly and Joining
- Automation and Robotics
- Bending and Forming
- Consumables
- Cutting and Weld Prep
- Electric Vehicles
- En Español
- Finishing
- Hydroforming
- Laser Cutting
- Laser Welding
- Machining
- Manufacturing Software
- Materials Handling
- Metals/Materials
- Oxyfuel Cutting
- Plasma Cutting
- Power Tools
- Punching and Other Holemaking
- Roll Forming
- Safety
- Sawing
- Shearing
- Shop Management
- Testing and Measuring
- Tube and Pipe Fabrication
- Tube and Pipe Production
- Waterjet Cutting
Industry Directory
Webcasts
Podcasts
FAB 40
Advertise
Subscribe
Account Login
Search
Sheet metal bending calculation basics
Calculating bend allowance, outside setback, and bend deductions
- By Steve Benson
- Updated May 18, 2023
- November 9, 2012
- Article
- Bending and Forming
When a sheet metal part is bent, it physically gets bigger. The final formed dimensions will be greater than the sum total of the outside dimensions of the part as shown on the print—unless some allowance for the bend is taken into account. Many will say material “grows” or “stretches” as it is bent in a press brake. Technically, the metal does neither, but instead elongates. It does this because the neutral axis shifts closer to the inside surface of the material.
The neutral axis is an area within the bend where the material goes through no physical change during forming. On the outside of the neutral axis the material is expanding; on the inside of the neutral axis the material is compressing. Along the neutral axis, nothing is changing—no expansion, no compression. As the neutral axis shifts toward the inside surface of the material, more material is being expanded on the outside than is being compressed on the inside. This is the root cause of springback.
Sheet Metal Bending Calculation
Bend Allowance (BA)
BA = [(0.017453 × Inside radius) + (0.0078 × Material thickness)] × Bend angle, which is always complementary
The length of the neutral axis is calculated as a bend allowance, taken at 50 percent of the material thickness. In Machinery’s Handbook, the K-factor for mild cold-rolled steel with 60,000-PSI tensile strength is 0.446 inch. This K-factor is applied as an average value for most bend allowance calculations. There are other values for stainless and aluminum, but in most cases, 0.446 in. works across most material types.
If you multiply the material thickness by the K-factor (0.446), you get the location of the relocated neutral axis: for example, 0.062 × 0.446 = 0.027 in. This means that the neutral axis moves from the center of the material to a location 0.027 in. from the inside bend radius’s surface. Again, the neutral axis goes through no physical change structurally or dimensionally. It simply moves toward the inside surface, causing the elongation.
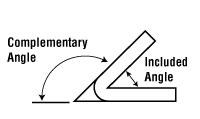
Note the two factors shown in the bend allowance formula: 0.017453 and 0.0078. The first factor is used to work your way around a circle or parts of a circle, and the second value applies the K-factor average to the first factor. The 0.017453 is the quotient of π/180. The 0.0078 value comes from (π/180) × 0.446. Note that for the bend allowance, the bend angle is always measured as complementary (see Figure 1).
Outside Setback (OSSB)
OSSB = [Tangent (Degree of bend angle / 2)] × (Inside bend radius + Material thickness)
The outside setback is a dimensional value that begins at the tangent of the radius and the flat of the leg, measuring to the apex of the bend (see Figure 2). At 90 degrees, it does not matter if you use the included or complementary angle; you still end up with 45 degrees, and you get the same OSSB answer.
For underbent angles (click here for Figure 3), it is common practice to use the complementary angle. For overbent (acute bend) angles, either the included or complementary angles may be used. The choice is yours, but it does affect how you apply the data to the flat pattern.
Bend Deduction (BD)
BD = (Outside setback × 2) – Bend allowance
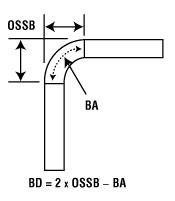
Figure 2: The outside setback (OSSB) is a dimensional value that begins at the tangent of the radius and the flat of the leg, measuring to the apex of the bend.
A bend deduction (BD) is the value subtracted from the flat blank for each bend in the part, and there may be more than one. Bend deductions differ depending on the part itself, different bend angles, and/or inside radii. Note that when overbending and making the OSSB calculation using the included bend angle, you may calculate a negative value for the bend deduction. You will need to take the negative value into account when calculating the flat blank, as discussed in the next section.
Development of the Flat-blank Layout
There are two basic ways to lay out a flat blank, and which to use will depend on the information that you are given to work with. For the first method, you need to know the leg dimensions. A leg is any flat area of a part, whether it is between bend radii or between an edge and a bend radius. For the second method, you need to know the dimension from the edge (formed or cut) to the apex of the bend, or the intersection created by both planes that run parallel to the outside surfaces of the formed material.
1. Flat blank = First leg dimension + Second leg dimension + Bend allowance
2. Flat blank = Dimension to apex + Dimension to apex – Bend deduction
There is another way to look at the second option. As mentioned earlier, if you use the included angle for the OSSB, the bend deduction may be a negative value. As you may know, subtracting a negative value requires you to add: for example, 10 – (-5) = 15. If you are working the formula on your calculator, it will automatically make the proper calculations. If you are working the formula through line by line, you will need to keep track of the answer’s sign and whether it is positive or negative.
The following examples walk you through the flat-blank development methods. They apply bend functions to a simple, single-bend part, bent past 90 degrees complementary, to show how the complementary or included angles are applied in the OSSB and ultimately to a layout.
The part in Figure 4 is bent to 160 degrees complementary. It has a material thickness of 0.250 in. and an inside bend radius of 0.250 in. The legs are each 1.000 in., and the dimension to the apex (between the part edge and bend apex) is 3.836 in. Note that in the formulas below, Ir represents the inside bend radius and Mt represents the material thickness. For all methods, we calculate the bend allowance the same way:
Bend Allowance (BA)
BA = [(0.017453 × Ir) + (0.0078 × Mt)] × Degree of bend angle complementary
BA = [(0.017453 × 0.25) + (0.0078 × 0.25)] × 160
BA = [0.00436325 + 0.00195] × 160
BA = 0.00631325 × 160
BA = 1.010
From here, we perform different calculations, depending on the flat-blank development used. Using the first method, we develop the flat blank by adding the two legs of the bend and the bend allowance.
Flat-blank Calculation
Calculated flat-blank length = Leg + Leg + BA
Calculated flat-blank length = 1.000 + 1.000 + 1.010
Calculated flat-blank length = 3.010
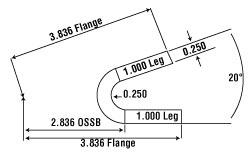
Figure 4: This 0.250-in.-thick part is bent to 160 degrees complementary with an inside bend radius of 0.250 in. The drawing specifies that the dimension from the edge to the apex is 3.836 in.
The second flat-blank-development example adds the two dimensions (from edge to the apex), and subtracts a bend deduction. In this case, the calculations use a complementary angle for the OSSB, and the dimensions are called from the edge to the apex—again, as specified in Figure 4.
Outside Setback (OSSB)
OSSB = [Tangent (complementary bend angle/2)] × (Mt + Ir)
OSSB = [Tangent (160/2)] × (0.25 + 0 .25)
OSSB = [Tangent 80] × 0.5
OSSB = 5.671 × 0.5
OSSB = 2.836
Bend Deduction
BD = (OSSB × 2) – BA
BD = (2.836 × 2) – 1.010
BD = 5.672 – 1.010
BD = 4.662
Flat-blank Calculation
Calculated flat blank = Dimension to apex + Dimension to apex – Bend deduction
Calculated flat blank = 3.836 + 3.836 – 4.662
Calculated Flat-blank Length = 3.010
In this final example, the flat-blank calculation adds the dimensions and then subtracts the negative bend deduction (again, you add when subtracting a negative number). In this case, we are using the included angle for the OSSB, and the dimensions are still called from the edge to the apex.
Outside Setback (OSSB)
OSSB = [Tangent (Degree of bend angle included/2)] × (Mt + Ir)
OSSB = [Tangent (20/2)] × (0.25 + 0.25)
OSSB = [Tangent 10] × 0.5
OSSB = 0.176 × 0.5
OSSB = 0.088
Bend Deduction (BD)
BD = (OSSB × 2) – BA
BD = (0.088 × 2) – 1.010
BD = 0.176 – 1.010
BD = -0.834
Flat-blank Calculation
Calculated flat blank = Dimension to apex + Dimension to apex – Bend deduction
Calculated flat blank = 1.088 + 1.088 – (-0.834)
Calculated flat-blank length = 3.010
You can see that regardless of method, the same answer is achieved. Be sure you are calculating these values based on the actual radius you are attaining in the physical part. There are many extenuating circumstances you may need to consider. Just a few are the forming method (air forming, bottoming, or coining), the type of bend (sharp, radius, or profound radius bends), the tooling you are using, and the multibreakage of the workpiece during large-radius bending. Also, the farther past 90 degrees you go, the smaller the inside radius will physically become. You can calculate for most of these, and this is something we’ll be sure to tackle in future articles.
Getting the Part Right the First Time
There are lots of different paths to find your way around a bend, by using either the included or complementary angles. We can easily calculate these values; it is the application of the results that counts. However, once you know how and where the information is applied in a given situation, the flat-pattern layout is easy.
So why calculate all these values? Because sometimes you will need to work your way around a bend on a print, and you may not have all the information you need to complete a flat pattern. At least now you can calculate all the different parts of the bend, apply them correctly, and get it right the first time.
More Than One Sheet Metal Bending Formula
Press brake technicians can use various formulas to calculate bend functions. For instance, in this article we have used the following for outside setback: OSSB = [Tangent (degree of bend angle/2)] × (Material thickness + Inside radius). However, some may use another formula: OSSB = (Material thickness + Inside radius) / [Tangent (degree of bend angle/2)]. So which is right? Both are. If you use the complementary bend angle in the first equation and the included angle in the second equation, you get the same answer.
Consider a part with a 120-degree complementary bend angle, a material thickness of 0.062 in., and an inside radius of 0.062 in. The bend allowance (BA) is calculated at 0.187, and the leg lengths are 1.000 in. To obtain the dimension to apex, add the OSSB to the leg. As you can see, both OSSB formulas produce the same result and lead you to the same bend deduction for calculating the flat blank.
First OSSB Formula
OSSB = [Tangent (degree of bend angle complementary/2)] × (Material thickness + Inside radius)
OSSB = [Tangent (120/2)] × (0.062 + 0.062)
OSSB = [Tangent (60)] × 0.124
OSSB = 1.732 × 0.124
OSSB = 0.214
OSSB = (Material thickness + Inside radius) / [Tangent (degree of bend angle included/2)]
OSSB = (0.062 + 0.062)/[Tangent (60/2)]
OSSB = 0.124/[Tangent (30)]
OSSB = 0.124/0.577
OSSB = 0.214
Bend Deduction (BD)
BD = (OSSB × 2) – BA
BD = (0.214 × 2) – 0.187
BD = 0.428 – 0.187
BD = 0.241 in.
Flat-blank Calculation
Calculated flat-blank length = Dimension to apex + Dimension to apex – Bend deduction
Calculated flat-blank length = (OSSB + Leg) + (OSSB + Leg) – Bend deduction
Calculated flat-blank length = (0.214 + 1.000) + (0.214 + 1.000) – 0.241
Calculated flat-blank length = 1.214 + 1.214 – 0.241
Calculated flat-blank length = 2.187 in.
For overbent angles (see Figure 3), the original formula—OSSB = [Tangent (degree of bend angle complementary/2)] × (Material thickness + Inside radius)—also may be written using the included degree of bend angle. But again, when you get a negative bend deduction value, you need to take that into account when calculating the flat blank.
Working with an included bend angle of 60 degrees, a material thickness of 0.062 in., an inside bend radius of 0.062 in., and a bend allowance (BA) of 0.187 in., you get a negative bend deduction. That means you subtract the negative BD (again, the same as adding) when doing the flat-blank calculation. As you can see, the same calculated flat-blank dimension results:
Outside Setback (using included angle)
OSSB = [Tangent (degree of included bend angle/2)] × (Material thickness + Inside radius)
OSSB = [Tangent (60/2)] × (0.062 + 0.062)
OSSB = [Tangent (30)] × 0.124
OSSB = 0.577 × 0.124
OSSB = 0.071
Bend Deduction (BD)
BD = (OSSB × 2) – BA
BD = (0.071 × 2) – 0.187
BD = 0.142 – 0.187
BD = -0.045
Flat-Blank Calculation
Calculated flat-blank length = Dimension to apex + Dimension to apex – Bend deduction
Calculated flat-blank length = (Leg + OSSB) + (Leg + OSSB) – BD
Calculated flat-blank length = (1.000 + 0.071) + (1.000 + 0.071) – (-0.045)
Calculated flat-blank length = 1.071 + 1.071 – (-0.045)
Calculated flat-blank length = 2.187 in.
About the Author

Steve Benson
2952 Doaks Ferry Road N.W.
Salem, OR 97301-4468
503-399-7514
Related Companies
subscribe now

The Fabricator is North America's leading magazine for the metal forming and fabricating industry. The magazine delivers the news, technical articles, and case histories that enable fabricators to do their jobs more efficiently. The Fabricator has served the industry since 1970.
start your free subscription- Stay connected from anywhere

Easily access valuable industry resources now with full access to the digital edition of The Fabricator.

Easily access valuable industry resources now with full access to the digital edition of The Welder.

Easily access valuable industry resources now with full access to the digital edition of The Tube and Pipe Journal.
- Podcasting
- Podcast:
- The Fabricator Podcast
- Published:
- 04/16/2024
- Running Time:
- 63:29
In this episode of The Fabricator Podcast, Caleb Chamberlain, co-founder and CEO of OSH Cut, discusses his company’s...
- Trending Articles
Tips for creating sheet metal tubes with perforations

JM Steel triples capacity for solar energy projects at Pennsylvania facility

Are two heads better than one in fiber laser cutting?

Supporting the metal fabricating industry through FMA

Omco Solar opens second Alabama manufacturing facility

- Industry Events
16th Annual Safety Conference
- April 30 - May 1, 2024
- Elgin,
Pipe and Tube Conference
- May 21 - 22, 2024
- Omaha, NE
World-Class Roll Forming Workshop
- June 5 - 6, 2024
- Louisville, KY
Advanced Laser Application Workshop
- June 25 - 27, 2024
- Novi, MI